La cotation d'une obligation
Les titres obligataires sont, dans leur écrasante majorité, cotés soit avec leur prix pied de coupon, soit avec leur taux de rendement.
La méthode utilisée pour chaque type de papier suit les conventions de marché.
Ainsi, pour la zone Euro, les obligations couponnées de moyenne ou longue durée sont cotées en pourcentage du nominal, les zéro coupons, indépendamment de leur durée de vie, ainsi que les obligations courtes (moins de deux ans) et les bons (titres courts, relevant plutôt du marché monétaire) sont cotés en taux de rendement.
Ce n’est qu’une simple convention de marché, on peut, comme nous allons voir par la suite, aisément convertir l’un en l’autre. Pour analyser une obligation on se base d’ailleurs toujours sur le taux de rendement, qui rend une comparaison entre différents titres possible, ce qui n’est pas le cas en se basant sur le prix.
Il existe également des titres dont le prix est coté en euros. Il s’agit, à part quelques titres exotiques, essentiellement d’obligations convertibles, qui ne nous intéressent pas ici.
Détermination du prix d’une obligation
Le schéma de flux d’une obligation
Le prix, exprimé en pourcentage du nominal, d’une obligation n’est rien d’autre que l’expression de la valeur actuelle de l’ensemble des flux auquel il donne droit, c'est-à-dire les flux d’intérêt (= coupons) et le remboursement du nominal, qui a lieu généralement en une seule fois à l’échéance. Nous allons illustrer cela en dessinant un schéma des d’une obligation, en l’occurrence l’OAT 4% 25-04-2014 (Code ISIN : FR0010061242) :
Ce schéma montre les flux d’intérêts de 4% qui sont versés chaque année. Ce flux est majoré pour la dernière année du remboursement du principal de l’obligation, qui est de 100% du nominal, ce qui nous donne un flux de 104%.
La détermination de la valeur actuelle des flux
La valeur actuelle des flux à venir est déterminée en les actualisant. La convention du marché veut qu’on actualise tous les flux à un taux unique.
Cela rend les choses plus faciles d’un point de vue calcul, mais cela ne correspond pas à la réalité économique des choses, puisqu’un flux prêté pendant un an ne le sera pas au même taux qu’un flux prêté durant cinq ans. Pourtant c’est cela que signifie l’actualisation de tous les flux au même taux.
Ce taux d’actualisation est le taux de rendement de l’obligation.
La formule utilisée pour l’actualisation des flux est la suivante:
Pointez sur la formule pour voir la légende
Le prix de l’obligation est donc obtenu en faisant la somme des flux de coupon (cpn) et du remboursement (C), actualisés chacun au taux de rendement i sur la période t, qui est, pour chaque flux, la durée (en années) entre la date d’achat et la date de tombée du flux.
| Titre | OAT 4% 25-04-2014 |
| Coupon facial | 4.000% |
| Echéance | 25 avril 2014 |
| Taux de rendement actuariel | 2.450% |
| Convention de base | Exact/Exact |
| Jours d'intérêt couru | 173 (du 25-04-2009 au 15-10-2009) |
| Jours d'intérêt restants à courir | 192 (du 15-10-2009 au 25-04-2010) |
| Fraction d'année | 0.526027 ( = 192 / 365 ) |
| Date de flux | Flux (cpn / C) | Période d'actualisation | Taux d'actualisation | Flux actualisé |
|---|---|---|---|---|
| 25-04-2010 | 4.000 | 0.526027 | 2.450% | 3.949 |
| 25-04-2011 | 4.000 | 1.526027 | 2.450% | 3.855 |
| 25-04-2012 | 4.000 | 2.526027 | 2.450% | 3.763 |
| 25-04-2013 | 4.000 | 3.526027 | 2.450% | 3.673 |
| 25-04-2014 | 104.000 | 4.526027 | 2.450% | 93.209 |
| Somme | 108.448 | |||
La valeur actuelle des flux futurs, et le prix coupon couru inclus de l’obligation, est de 108.448%. Afin d’obtenir le prix pied de coupon (ou clean price) qui est le prix réellement affiché, il faut soustraire les intérêts courus.
Différence entre le prix coupon couru inclus (gross price) et le prix pied de coupon (clean price)
Comme il a déjà été évoqué, le prix obtenu en appliquant la formule ci-dessus est le prix coupon couru inclus, en anglais gross price. Mais ce n’est pas le prix qu’on lira dans un journal économique ou sur une page Bloomberg, Reuters ou autre comme étant le prix coté de l’obligation. Le prix affiché et toujours le prix pied de coupon, ou clean price. Pour illustrer la différence, nous allons nous servir de l’exemple ci-dessus, et regarder ce point en détail.
Le triangle au-dessus de la ligne temps représente la valeur des intérêts courus, croissants de manière linéaire chaque jour. Cette valeur tombe à zéro à la date de tombée du coupon.
L’acquéreur de l’obligation n’aura droit aux intérêts qu’à partir de la date d’acquisition (dans notre exemple le 15 octobre 2009). Comme il recevra, le 25 avril 2010, le coupon intégral couvrant la période du 25 avril 2009 au 25 avril 2010, il doit régler au vendeur la partie des intérêts correspondant à la période entre le 25 avril et le 15 octobre, qui est de 173 jours. Leur valeur est calculée en multipliant le coupon nominal, 4%, par la fraction (nombre de jours d’intérêts courus / nombre de jours de la période), soit (173/365).
Elle ressort donc à 4% x (173/365) = 1.896%
En déduisant cette valeur de notre prix coupon couru inclus, nous obtenons le prix pied de coupon, ou clean price :
108.448% – 1.896% = 106.552%
La relation entre prix et taux de rendement
En regardant la formule pour le calcul du prix d’une obligation, on voit qu’il y a une relation étroite entre le prix et le taux de rendement du titre. Lorsque le taux de rendement augmente, le prix baisse et inversement. Voici cette relation sous forme de graphe à l'exemple d'une obligation ayant une maturité de 10 ans et un taux de coupon de 5% :
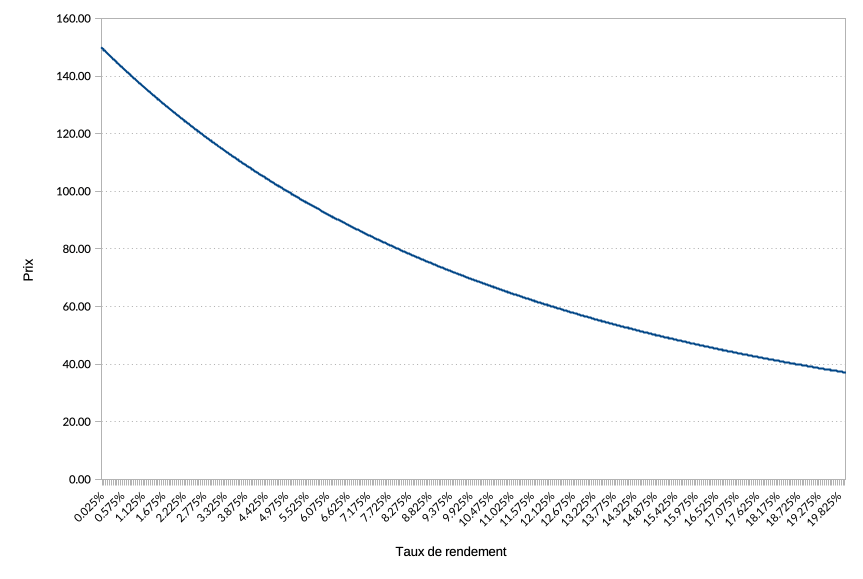
A noter que l’obligation cotera à 100% du nominal (on utilise également l’expression “au pair”), lorsque le taux de rendement aura la même valeur que le taux de coupon facial.


